This chapter is all about building fault tolerant distributed systems. We will look at tow measures for these - Consistency and consensus.
Consensus means all nodes of a distributed system agree on something(leader election, state of data etc.).
Consistency means the state of system is same across any node of distributed system. Eventual consistency is weak guarantee but stronger gurantees reduce performance.
Lets dive into consistency first. We will look at linearizability which is a strong consistency guarantee.
Linearizability
The basic idea behind linearizability is simple: to make a system appear as if there is only a single copy of the data. We will explore the concept with an image processing system.
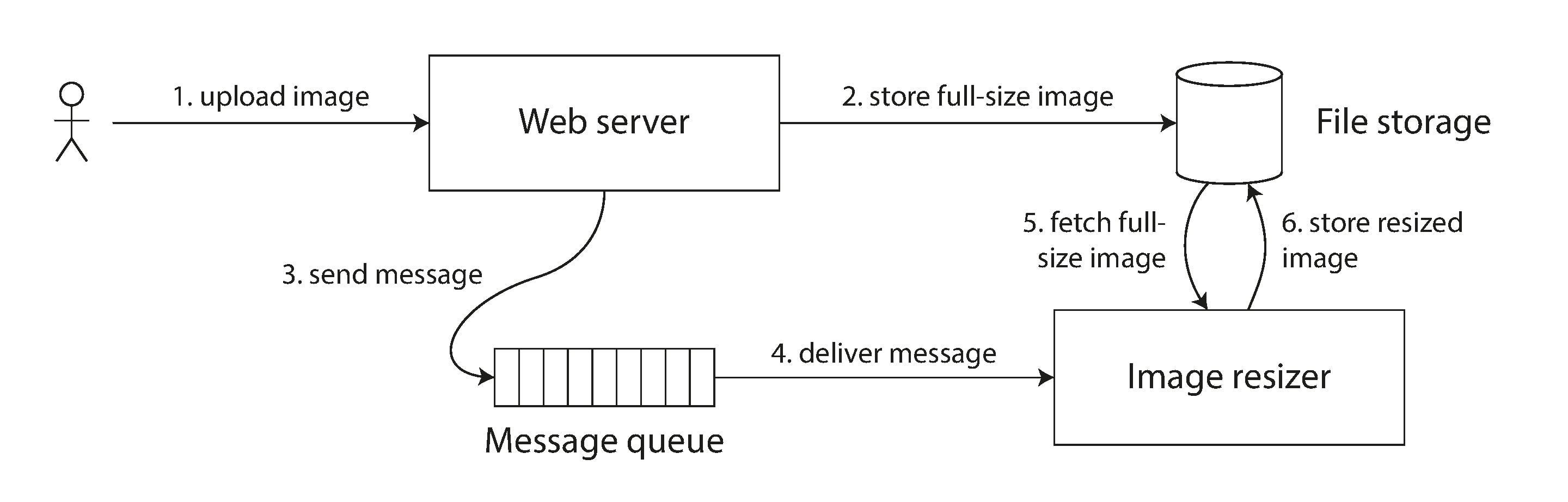
These are the steps in the architecture
- Upload image to web server
- Full image is stored in distributed storage system(eg: S3)
- Message containing image metadata is placed onto queue
- Image resizer fetches the image from queue and does resizing
User can upload multiple versions of the image (v1,v2,v3). Assume in very short succession images are uploaded. Storage has replication for fault tolerance and performance. They should be processed in order or else there is risk of resizer processing an old version of the image. This property of the storage system is called linearizable.
Linearizability looks similar to serializability but they are not. The latter is about transaction isolation while former is about single object. Linearizability is useful for enforcing constraints and uniqueness guarantees. For example when registering for website, each user must have unique username.
Lets see some of the common replication activities and discuss if they are linearizable
- Single-leader replication -> Linearizable. All writes go through leader and follower is used for back up copies of data
- Consensus algorithms -> Linearizable. We will discuss them in detail below
- Multi-leader replication -> Not Linearizable. Many leaders are processing writes and not possible to present single state at all times
- Leaderless replication-> Not Linearizable. Linearizable read and write operations can be implemented with quorums and performance impact. A linearizable compare-and-set operation cannot, because it requires a consensus algorithm.
How do we ensure linearizability in a distributed system ? The solution to the puzzle is ordering.
Ordering
Causality imposes an ordering on events: cause comes before effect. If a system obeys the ordering imposed by causality, we say that it is causally consistent. Causality is not total ordering.
Lets discuss this with the example of image processing. Assume user uploads Image 1 v1 followed by Image1 v2 and Image2 v1 simultaneously. We cannot compare image1v2 and image2 v1. We can process any of them first.
Linearizability is stronger than causal consistency. How do we ensure causality? Via timestamps of course. These can come from logical clock instead of physical clock.(Lamport Logical clock).
This approach has a problem. Lets discuss with an example of creating an username for the application. We can check if the username is already taken. What if two people choose the same username at the same time ?
We have to check with all nodes at the same time to determine if our timestamp is lesser than the other one. This is non trivial operation and time consuming.
You can implement a linearizable compare-and-set operation by using total order broadcast as an append-only log
- Append a message to the log, indicating the username you want to claim.
- Read the log, and wait for the message you appended to be delivered back to you.
- Check for any messages claiming the username that you want.
- If the first message for your desired username is your own message, then you are successful
- If the first message for your desired username is from another user, you abort the operation.
This is because of total order broadcast. This guarantees that log entries are delivered to all nodes in the same order. Nodes will agree on the order using consensus protocols which we will discuss next.
Consensus
Consensus means getting several nodes to agree on something. It could be leader election or atomically commiting a single transaction.
We will understand consensus with a set of examples starting with atomic commit. Atomicity means all the operations in the transaction should either succeed or fail. There should be no partial success. This is easily achievable in case of single machine scenario. In a distributed system, this becomes difficult. What if few of the nodes commited while it failed in few other nodes ?
2 Phase commit
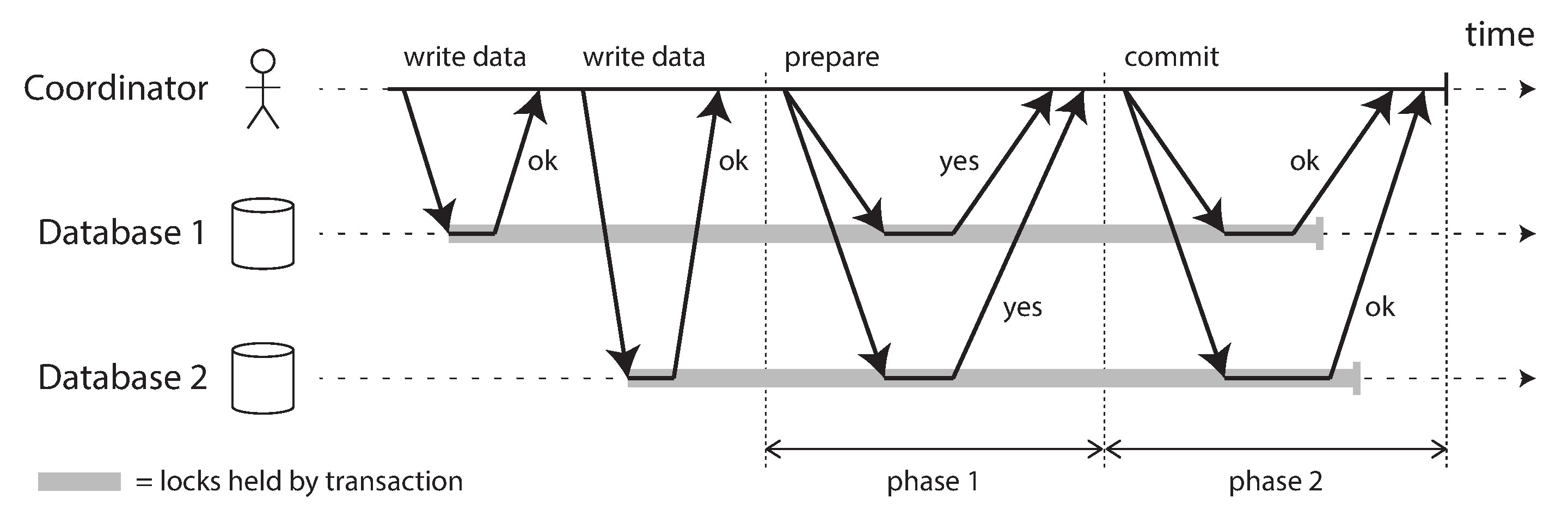
As the name implies there are two phases- prepare and commit phase. There is an extra component involved - coordinator. In phase1, coordinator asks other nodes whether they are ready to commit. These nodes are called participants.
- If all participants reply “yes,” then the coordinator sends out a commit request
- If any of the participants replies “no,” the coordinator sends an abort request
This reply phase and the next action is phase 2. Coordinator is the one finally sending the commit/ abort request to all nodes. If the coordinator fails without sending confirmation, still nodes abort the transaction.
X/A transactions
X/Open XA (short for eXtended Architecture) is a standard for implementing two-phase commit across heterogeneous technologies. It is same as 2PC discussed above but here coordinator library has to talk with two different systems - eg: database and message queue.
In theory, if the coordinator crashes and is restarted, it should cleanly recover its state from the log and resolve any in-doubt transactions. In some cases it fails and database will hold the lock waiting for coordinator. Practical solution is to use heuristic decisions -> allowing participant to decide to abort or commit an in-doubt transaction.
Limitations of distributed transactions
- Coordinator can be a single point of failure
- Coordinator needs to be a stateful application
- XA needs to interoperate with wide variety of systems and will be the lowest common denominator
- It amplifies failures i.e. if one participant fails entire transaction fails
Consensus Algorithms
A consensus algorithm must meet the following properties
- Uniform agreement - No two nodes decide differently.
- Integrity - No node decides twice.
- Validity - If a node decides value v, then some node proposed v.
- Termination - Every node that does not crash eventually decides some value.
Lets take an example of leader election. There is a single leader(n1) and 3 participants(n2,n3,and n4). The leader remains unreachable and other nodes have to take a decision.
n2 is being proposed as leader (n2 votes for itself)
- Uniform agreement - n3 and n4 agree
- Integrity - n3 and n4 cannot change their votes now
- Validity - n2 proposed the value and nodes agreed. It is not an arbitrary value
- Termination - All alive nodes participated.
what if n1 was just unresponsive and came back online ? To handle this problem epochs are used. Every time election happens, an epoch(monotonically increasing) number is used. Leader with greatest epoch is the current leader. A leader only proposes a value and majority of nodes have to agree. Thus, we have two rounds of voting: once to choose a leader, and a second time to vote on a leader’s proposal.
There are some subtle differences between consensus and 2PC
- A coordinator is always decided in 2PC and not elected
- Consensus needs a quorum of nodes to agree and not all nodes.
Consensus Limitations
- Consensus systems always need a strict majority to operate
- Dynamic membership extensions to consensus algorithms are complicated
- Consensus systems generally rely on timeouts to detect failed nodes. Consensus performs poorly in unpredictable networks due to frequent leader election
